[最も好ましい] (x-y)^3 (y-z)^3 (z-x)^3 factorise 358901-Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3
Use sum of cubes identity to find x^3y^3z^3 = (xyz)(x^2y^2xyzz^2) Use the sum of cubes identity a^3b^3=(ab)(a^2abb^2) with a=xy and b=z as follows x^3y^3z^3 =(xy)^3z^3 =((xy)z)((xy)^2(xy)zz^2) =(xyz)(x^2y^2xyzz^2)
Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3-Click here👆to get an answer to your question ️ Verify that x^3 y^3 z^3 3xyz = 1/2(x y z)(x y)^2 (y z) (z x)^2 Solve Study Textbooks Guides Join / Login >> Class 8 >> Maths >> Factorisation >> Factorisation >> Verify that x^3 y^3 z^3 3xyz = 1/2 Factorise x 2 2 xSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and more
Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 | 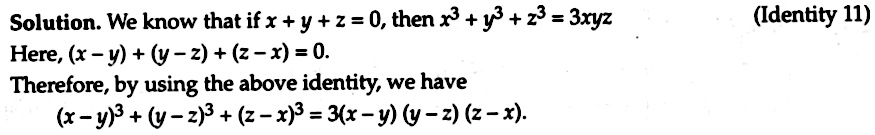 |  |
 |  |  |
 |  | |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
 | 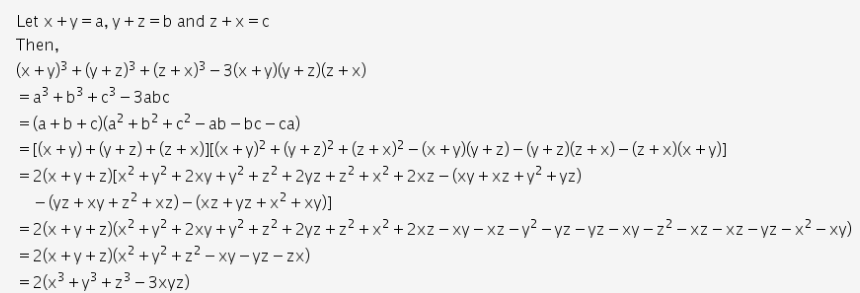 |  |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
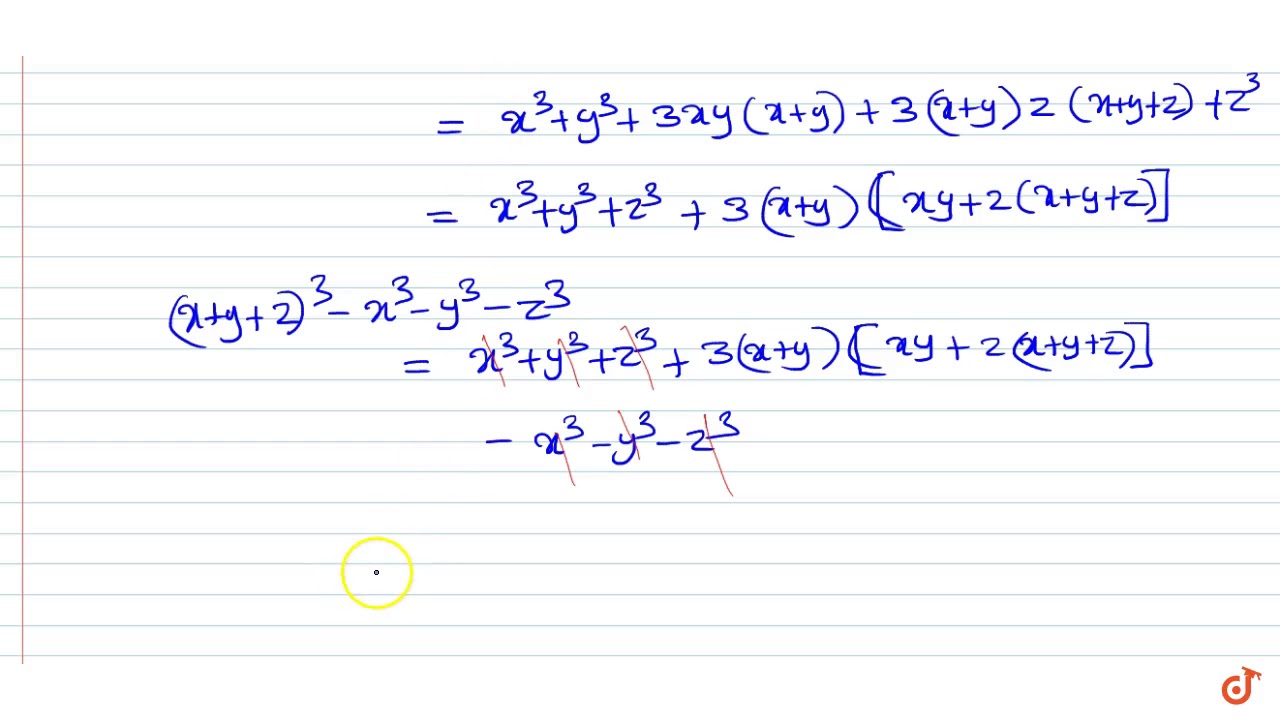 |  |  |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
 |  | |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
 |  | |
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 | ||
「Factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。
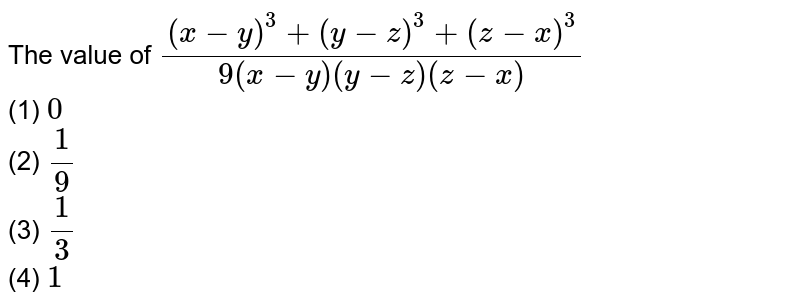 | 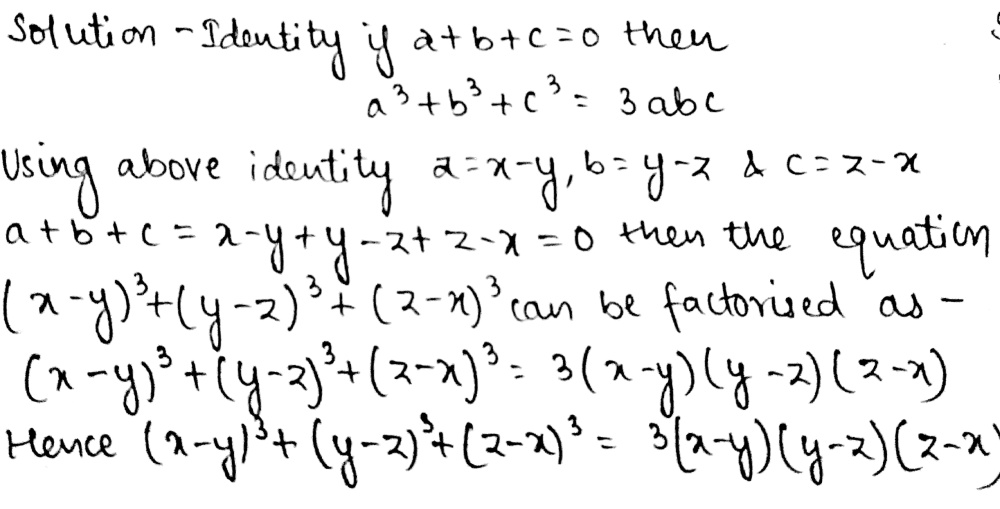 |  |
 |  |
p ( z) = z 3 − 3 x y ⋅ z x 3 y 3 So we can try our methods to factor a polynomial of degree 3 over an integral domain If it can be factored then there is a factor of degree 1, we call it z − u ( x, y) and u ( x, y) divides the constant term of p ( z) which is x 3 y 3The expression can be rewritten as \begin{align*} (x^3y^3)z&(z^3x^3)y(y^3z^3)x =(x^3y^3)z(z^3y^3y^3x^3)y(y^3z^3)x\\ & =(x^3y^3)(zy)(y^3z^3)(xy)\\ & =(xy)(zy)(x^2xyy^2)(xy)(yz)(y^2yzz^2)\\ &= (xy)(yz)(z^2yzx^2xy)\\ &= (xy)(yz)\bigl((zx)(zx)y(zx)\bigr)\\ &=(xy)(yz)(zx)(xyz) \end{align*}
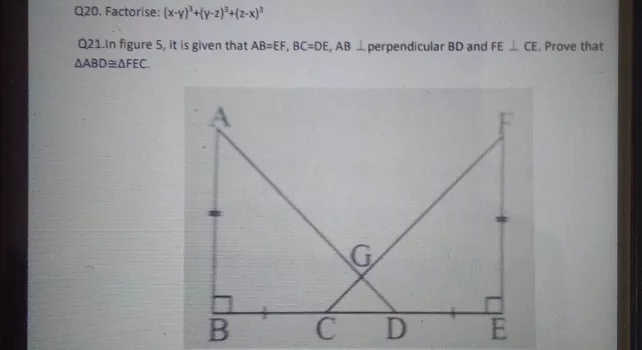
Incoming Term: (x-y)^3+(y-z)^3+(z-x)^3 factorise, without finding the cubes factorise (x-2 y)^3+(2y-z)^3+(z-x)^3, factorise the expression (x+y+z)^(3)-x^(3)-y^(3)-z^(3) into linear factors, factorise (2x-y-z)^3+(2y-z-x)^3+(2z-x-y)^3,




コメント
コメントを投稿